M1M3 mirror cell bump testing#
Abstract
To test the functionality of the pneumatic actuators on the M1M3 mirror cell, small perturbations are applied to each of the actuators in turn. This technote describes those tests and how to access the test results from the EFD. It also gives a short summary on the actuators with the highest rate of failures.
Introduction#
The M1M3 mirror cell supports the weight of the M1M3 primary mirror for the Simonyi telescope. The 17 tons of mirror are supported by 156 pneumatic actuators where 44 are single-axis and provide support only in the axial direction (parallel to the telescope optical axis), 100 are dual-axis providing support in the axial and lateral direction, and 12 are dual-axis providing support in the axial and cross lateral directions. Figures 1 and 2 show the locations of the actuators. Figure 2 shows the actuator types. Note that most of the dual-axis actuators apply force in the +Y direction. This is because this is the force needed to support the weight of the mirror as the telescope tilts to lower elevations.
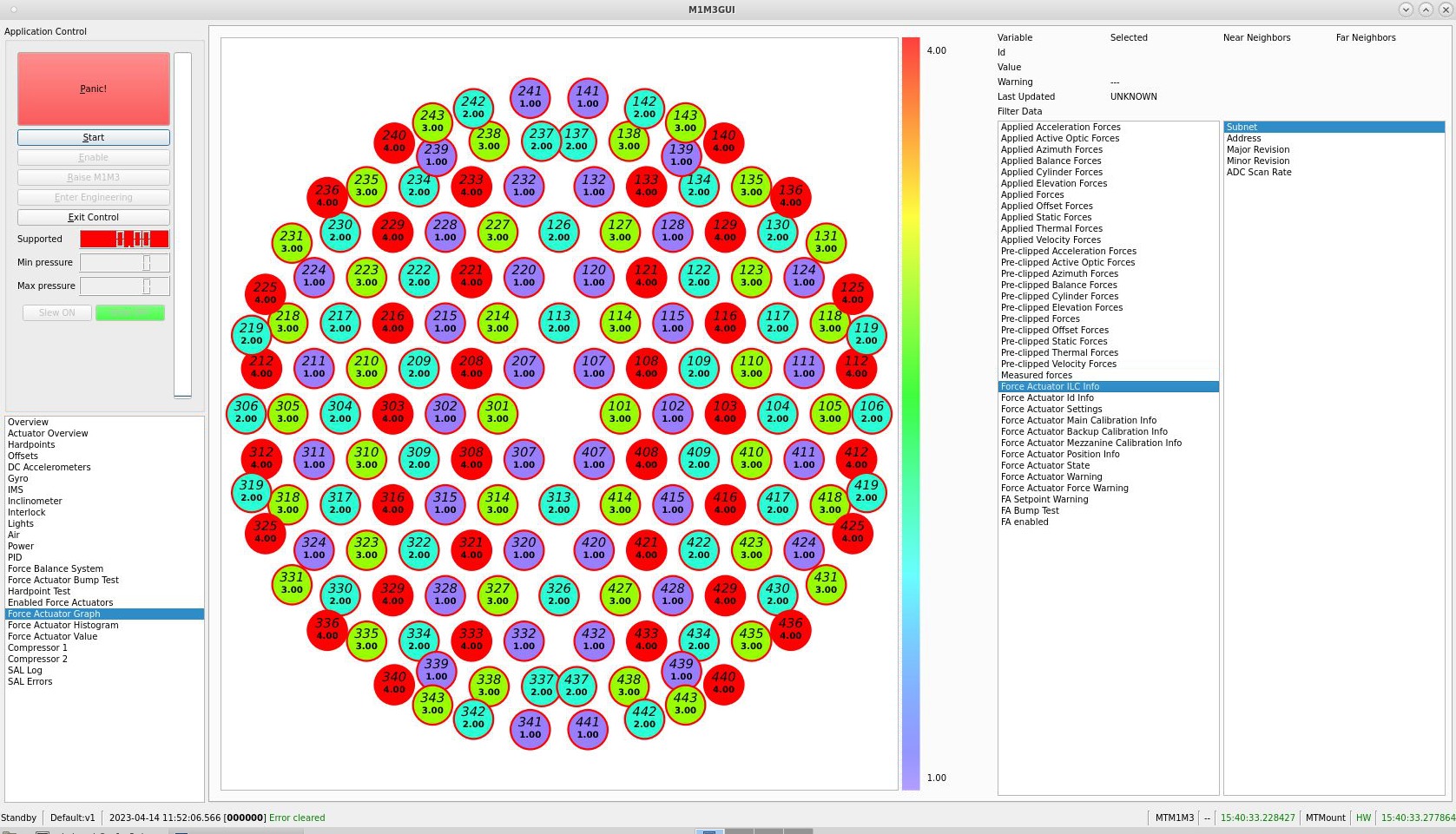
Figure 1. A screenshot of the MTM1M3 GUI, showing the actuator locations and IDs.
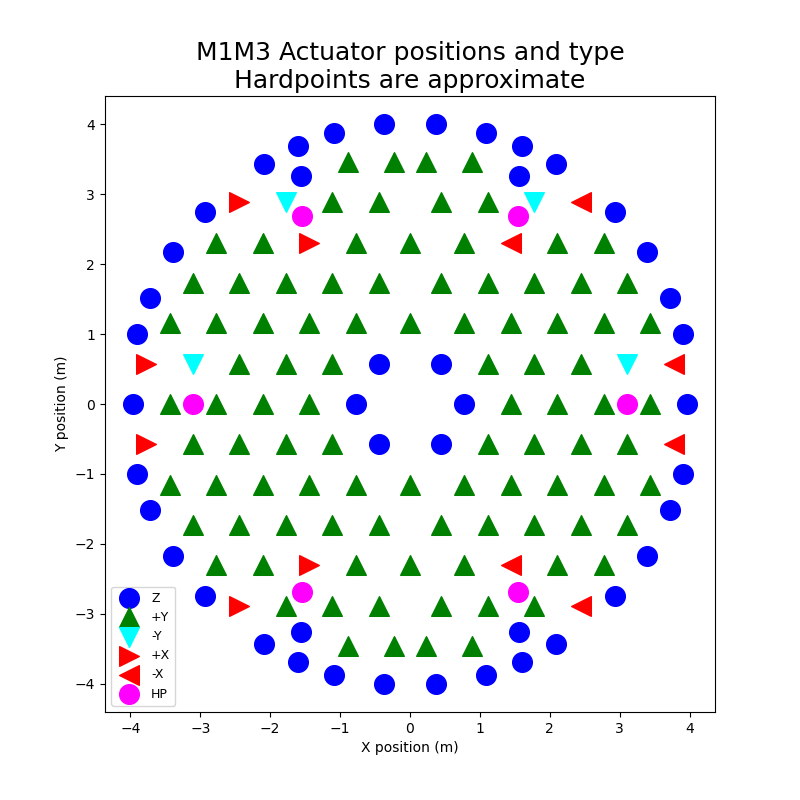
Figure 2. This figure shows the actuator types.
Positioning is provided by 6 hard points in a hexapod configuration which moves the mirror to a fixed operational position that shall be maintained during telescope operations. The remaining optical elements will be moved relative to this position in order to align the telescope optics. Support and optical figure correction is provided by the pneumatic actuators. Each actuator consists of a piston and valves to apply compressed air on either side of the piston, so that each actuator has the capability to push and pull.
To test the functionality of the actuators, there is a test applied to each actuator which is referred to as a “bump test”. This is usually performed with the mirror lowered (on static support), so the force actuators can be tested before the mirror is raised. The test is performed by applying an additional force of about 200 Newtons in both the positive and negative directions. For actuators that are dual-axis, the primary actuator (in the axial direction) is bumped first, followed by the secondary actuator. The bump test can be performed on either a single cylinder, or a single actuator, or it can be cycled through all of the actuators in succession.
Bump Test Overview#
During the bump test, perturbations of about 200 N are applied to the actuators for a few seconds. Figure 3 shows the target forces to be applied, and Figure 4 shows the actual measured forces.
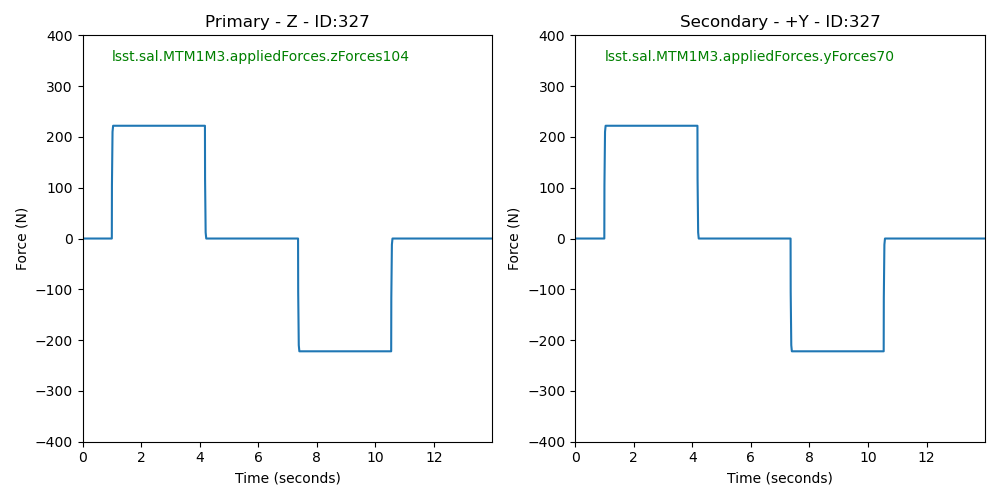
Figure 3. This shows the target forces to be applied to the actuators during the bump test of a single actuator.
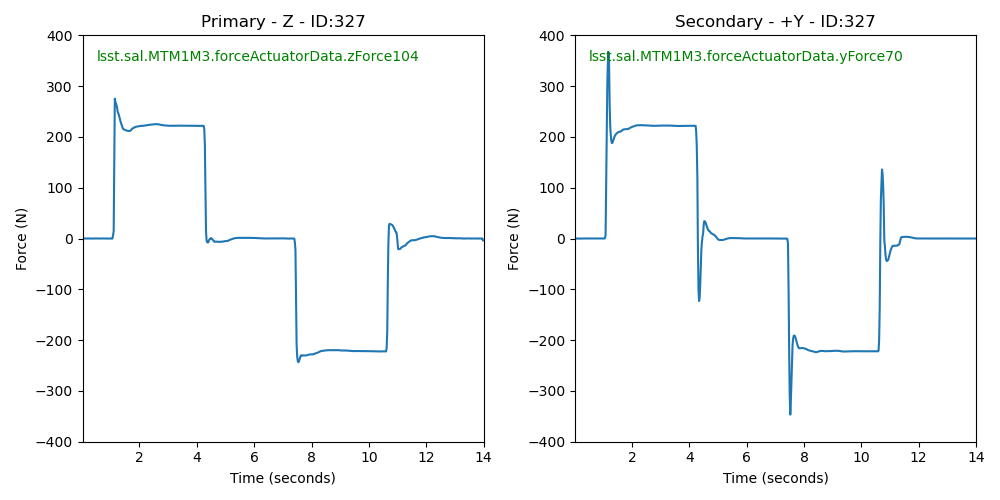
Figure 4. This shows the actual measured forces applied by the actuators during the bump test of a single actuator
Bump Test Indexing#
The actuators are numbered sequentially from 0-155. The secondary cylinders and the X, Y, and Z forces are also numbered sequentially. Since there are different numbers of each of these, a set of look-up tables are provided to go from the actuator ID to the sequential numbers of the actuators of different types. Table 1 shows how to move between the actuator IDs, the actuator index, and the indices for the various types of actuators.
from lsst.ts.xml.tables.m1m3 import actuator_id_to_index,FAIndex,FATable,force_actuator_from_id
Actuator ID (as in Figure 1): 101
actuator_id_to_index(101) : 0
force_actuator_from_id(101).index : 0
actuator_id_to_index(101, FAIndex.SECONDARY): None
force_actuator_from_id(101).s_index : None
actuator_id_to_index(102, FAIndex.SECONDARY): 0
force_actuator_from_id(102).s_index : 0
Actuator ID (as in Figure 1): 227
actuator_id_to_index(227) : 61
actuator_id_to_index(227, FAIndex.SECONDARY):46
actuator_id_to_index(227, FAIndex.Y):42
actuator_id_to_index(227, FAIndex.Z): 61
Since all actuators provide force in the Z direction, the ZINDEX and the INDEX are equal.
The following actuator is one of the 12 that provides force in the X direction.
Actuator ID (as in Figure 1): 135
actuator_id_to_index(135) : 34
actuator_id_to_index(135, FAIndex.X): 2
Table1: Navigating between actuator IDs and sequential indices.
Bump Test States#
As the bump test cycles through the testing, the EFD location:
returns where in the bump test cycle the test is. Figure 5 shows the progression of these states. At the conclusion of the test for each actuator, the state will either be 6 (PASSED) or 7 (FAILED). the pass-fail criteria are described later in the “Bump Test Following Errors” section.
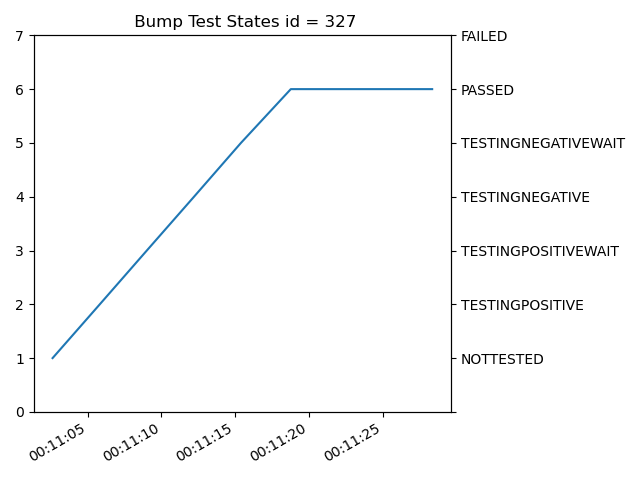
Figure 5. This shows the bump test states as logged in lsst.sal.MTM1M3.logevent_forceActuatorBumpTestStatus.
XYZ forces vs Cylinder forces#
The force data in the EFD includes both the forces applied to the primary and secondary cylinders, as well as the forces in the X, Y, and Z directions. The X, Y, and Z directions are in the mirror coordinate system, as described in this link (https://confluence.lsstcorp.org/pages/viewpage.action?pageId=47220348). The cylinder forces and the X, Y, Z forces are not the same, as will be explained in this section. Referring to Figure 6, we see that the primary cylinder applies force in the axial direction, which is along the optical axis of the telescope, and is referred to as the Z direction. So the force applied by the primary cylinder is equal to the Z-force. The secondary cylinder however, is at a 45 degree angle to the Z-axis. So if we want to apply a force in the lateral direction (X or Y), we need to apply a force with the secondary cylinder, and then a negative force with the primary cylinder so that the resultant is in the lateral direction. As the angle of the secondary cylinder is 45 degrees, transforming mirror coordinate systems forces into secondary cylinder is (mirror_force) / sqrt(2). Assume Z and Y Dual Axis Actuator (DAA) should produce Z force +10 N, and Y +25 N. Then the primary cylinder force would be 10 - (25 * sqrt(2)) N, and secondary cylinder force would be 25 * sqrt(2) N.
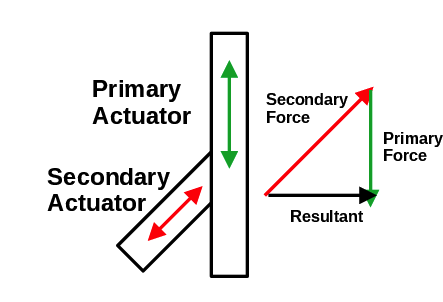
Figure 6. This schematic of the actuators shows the relation between the cylinder forces and the resulting axial and lateral forces.
The primary and secondary forces are what is actually measured, and the X, Y, and Z forces are calculated from these forces and the known geometry. So Figures 3 and 4 show the Y and Z forces. Figures 7 and 8 show the target and actual forces in the primary and secondary cylinders. Note the negative primary force being applied during the secondary bump test.
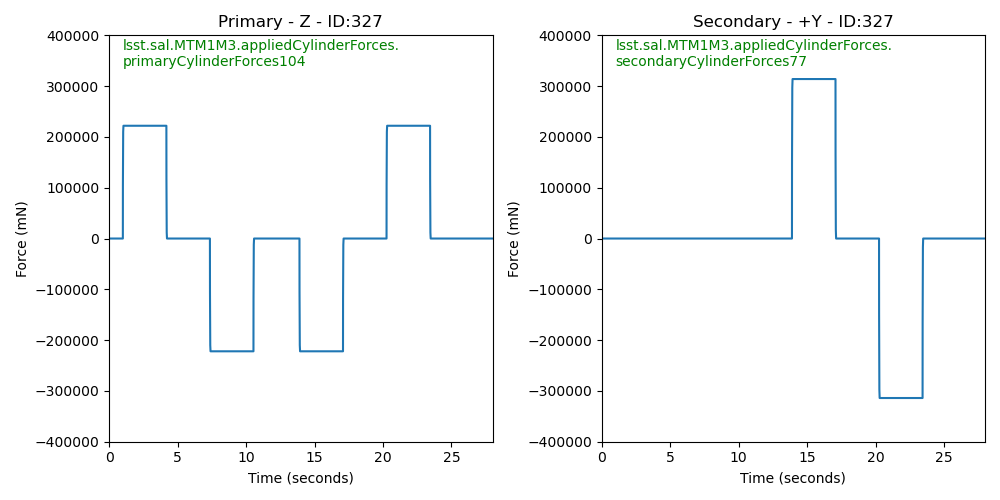
Figure 7. This shows the target forces to be applied to the primary and secondary actuators during the bump test of a single actuator.
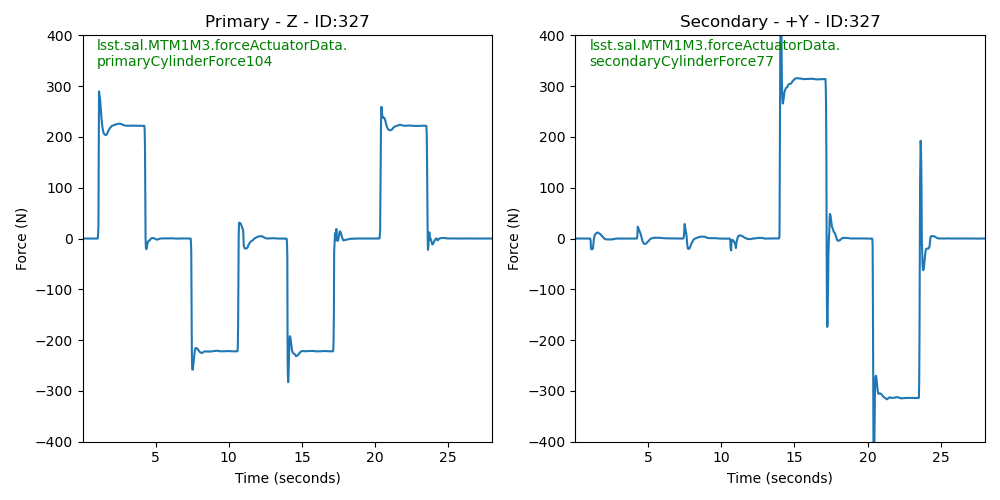
Figure 8. This shows the actual measured forces applied by the primary and secondary actuators during the bump test of a single actuator
Bump Test Following Errors#
We can also plot the bump test following errors, which are the difference between the target force and the actual measured force. The actuator is not able to follow the step function in the applied force, so there is large spike in the following error after a change in the target force. For this reason, the plot in Figure 9 uses the “symlog” scale, which is linear between -10 N and +10 N, and log above +/-10 N. This allows one to see the errors in the relatively flat region of the test, which is most important.
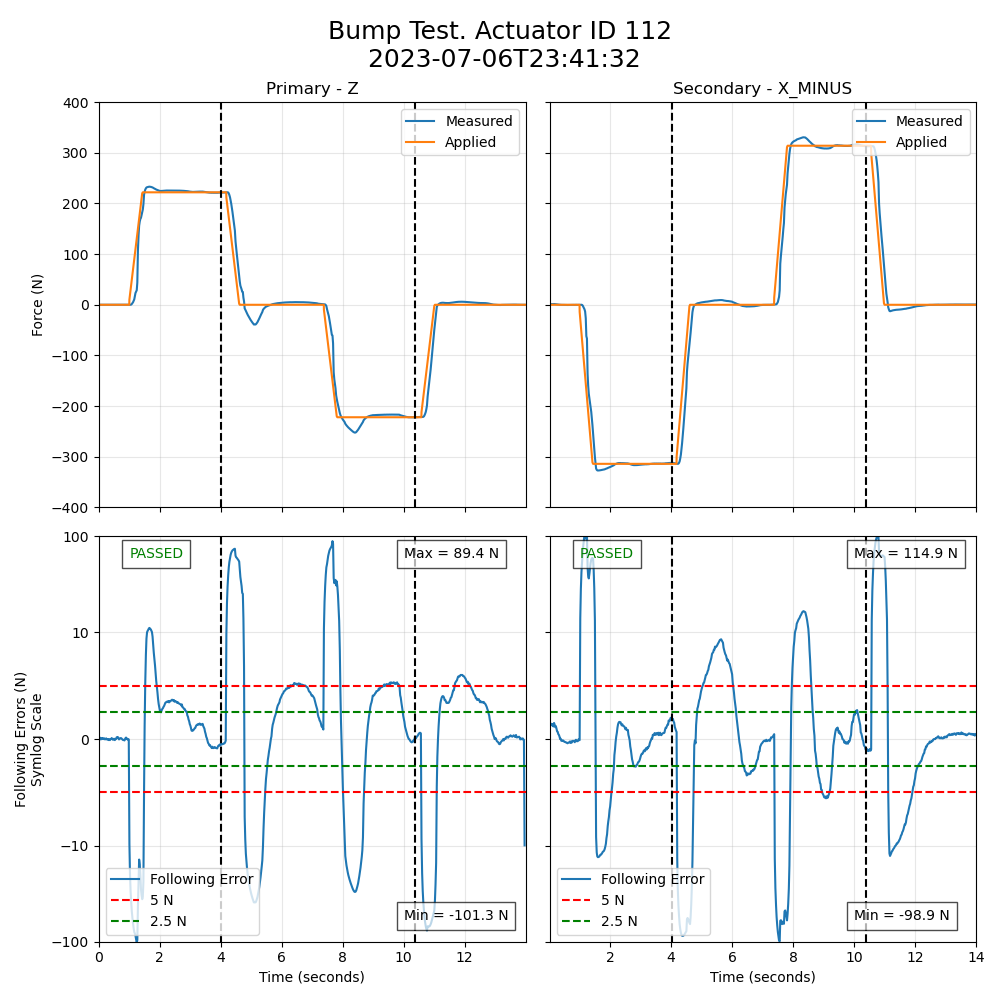
Figure 9. Bump test following errors. The dotted vertical line shows where the pass/fail decision is made (SettleTime below). If this is within the red lines (Error below), then the bump test passes.
The levels and times for the absolute value of the following error are specified in M1M3 SS CSC configuration file (ts_config_mttcs/MTM1M3/v1/_init.yaml):
Where non-tested mean all other Force Actuators (FAs)s (the algorithm checks if all other except for tested cylinder doesn’t show significant force), tested are error and warning levels for cylinder being tested. The algorithm waits up to SettleTime seconds to see “Measurements” number of measured absolute values dropping below errorr level for FA to pass the test. If measured values venture above “warning” level, but stay within “error” level, a warning is sent into the M1M3 log.
Trouble makers#
In order to determine which actuators causes more trouble, we calculated the rate of failures for all Bump Tests available in the efd to the date. The results are shown in Figure 10. At this point, we are interested in knowing the relative frequency of failures, which will give us an idea of the actuators with the highest rate of failures when compared to the total number of failures.
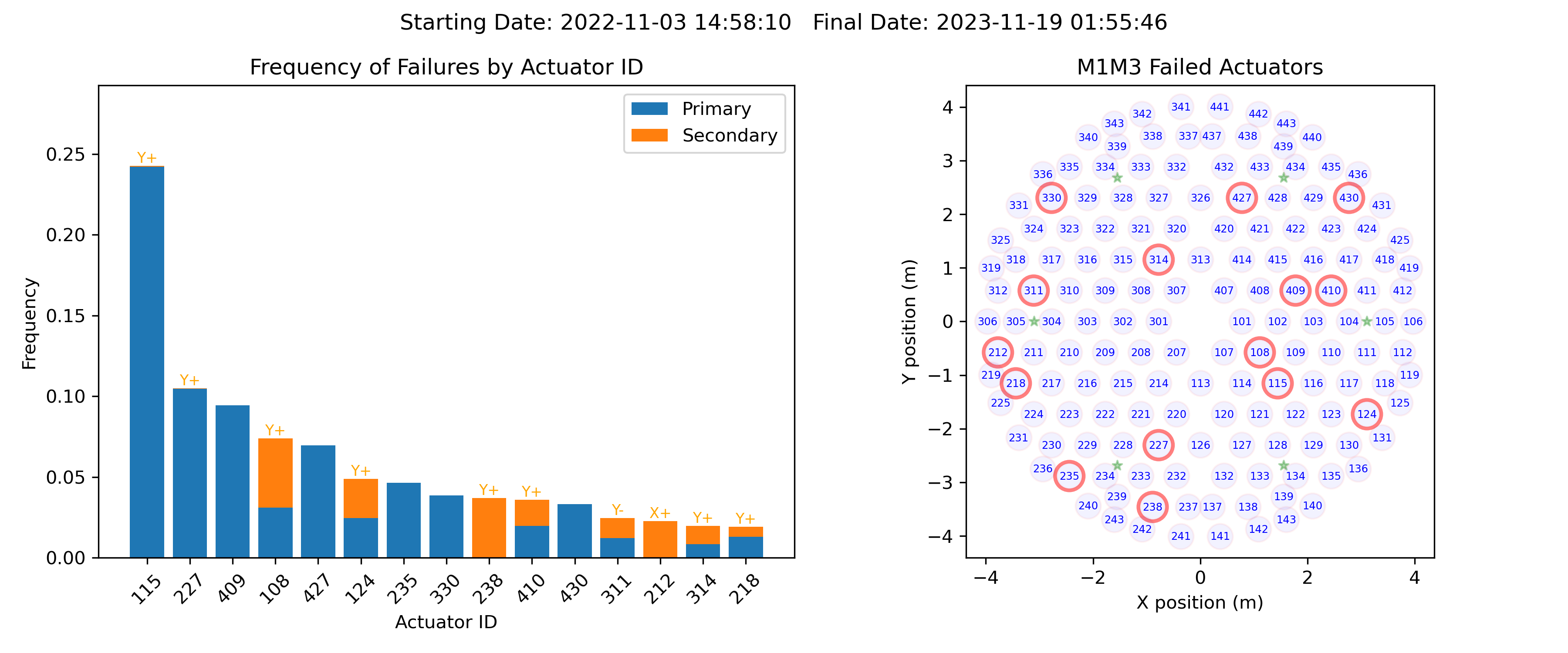
Figure 10. Frequency of failures with spatial distribution of the actuators. The direction of the Secondary failures are shown in orange on top of the corresponding bar. As stated above, Primary actuators will always have failures in the Z direction.
The Figure 11 shows the same result as the histogram from Figure 10, but now highlighting the spatial distribution of the actuators with the relative frequency of failures. It shows that no quadrant has more failures than the others. However, the actuators with the highest failure rate seem to be located towards the inner half of the M1M3 mirror, with a tendency to be along the +X TMA axis. Secondary failures seem to be more concentrated towards the -Y TMA axis direction.
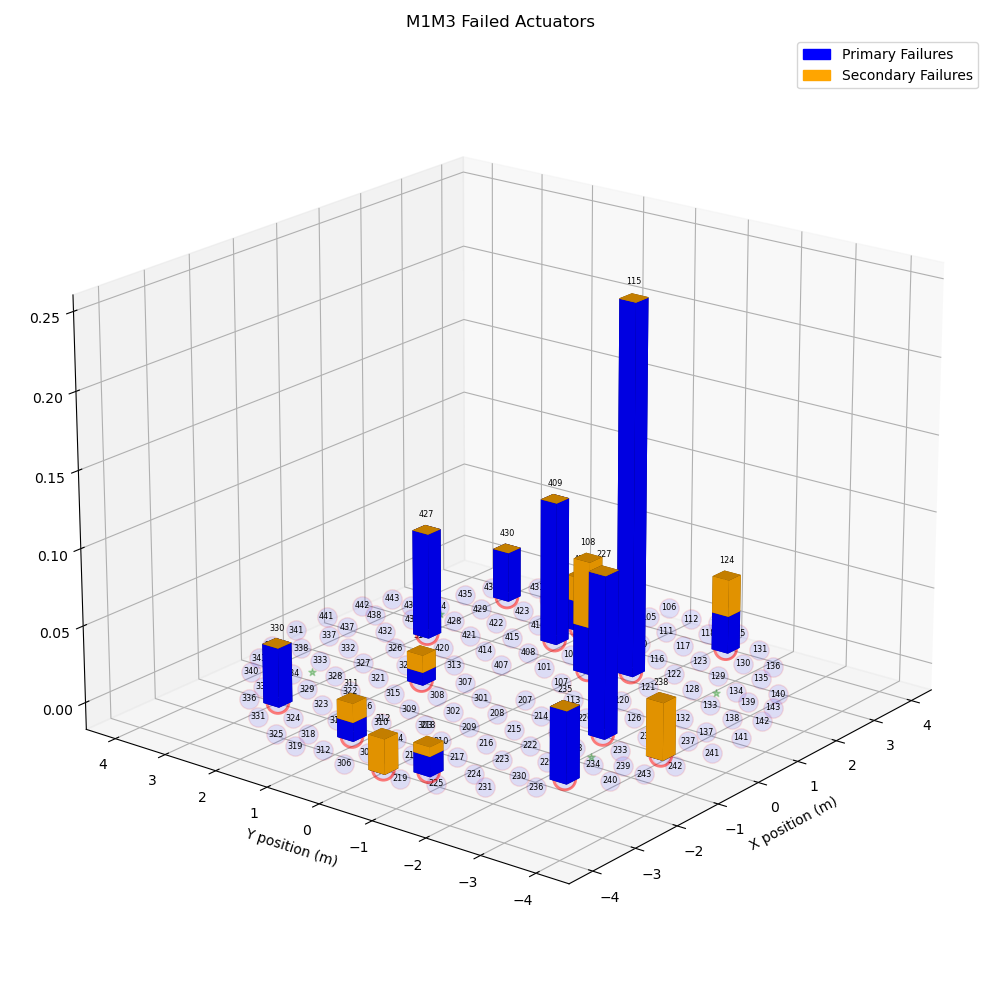
Figure 11. Distribution of the relative frequency of failures.
At this time (November 2023), we do not have the full set of Bump Tests available in the efd. Therefore, the results shown above are not representative of the full history of the M1M3 Bump Tests. In a separate analysis, we will look at the full history of the Bump Tests, taking into account that a few actuators have been replaced over the past 1-2 years.
In this follow-up analysis, we will look at the absolute frequency of failures, which will tell us how often a given actuator fails a Bump Test. We will also track the individual history of each actuator (based on position), comparing its behavior before and after any replacements.
Types of bump test failures#
David Sanmartim has written code to find and characterize all of the bump test failures between 2023-11-01 and 2024-01-15. The nights between 2023-11-09 and 2023-12-12 were omitted because there were some unexplained failures. This represents 164 different bump test failures. Table 2 shows the type of information available from the EFD. Figures 12, 13, 14, and 15 show different ways to look at the failures. Table 3 also shows high-level statistics of all of the bump test failures.
In the data directory of this technote is a set of plots of all of the bump test failures, labeled Bump_Test_Failures_01Apr24.pdf.
Time: 2023-11-30 00:00:00
ID: 235
Orientation: Z
Index: 69
Error Message: measured force plus (204.525) is too far 222±5
MeasuredForce: 204.525
AppliedForceDirection: Positive
Deviation: -17.475
AbsMeasuredForce: 204.525
DaysSinceFirst: 22
Table 2: Information on bump test failures in the EFD
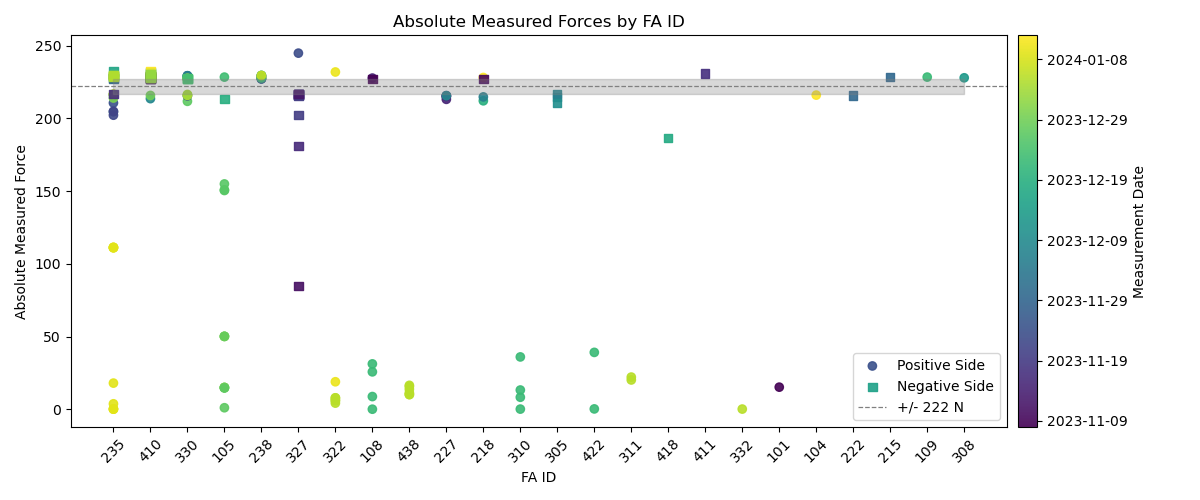
Figure 12. Absolute Measured Forces by FA ID.

Figure 13. Average Deviation with Dispersion by Actuator ID and Error Type.
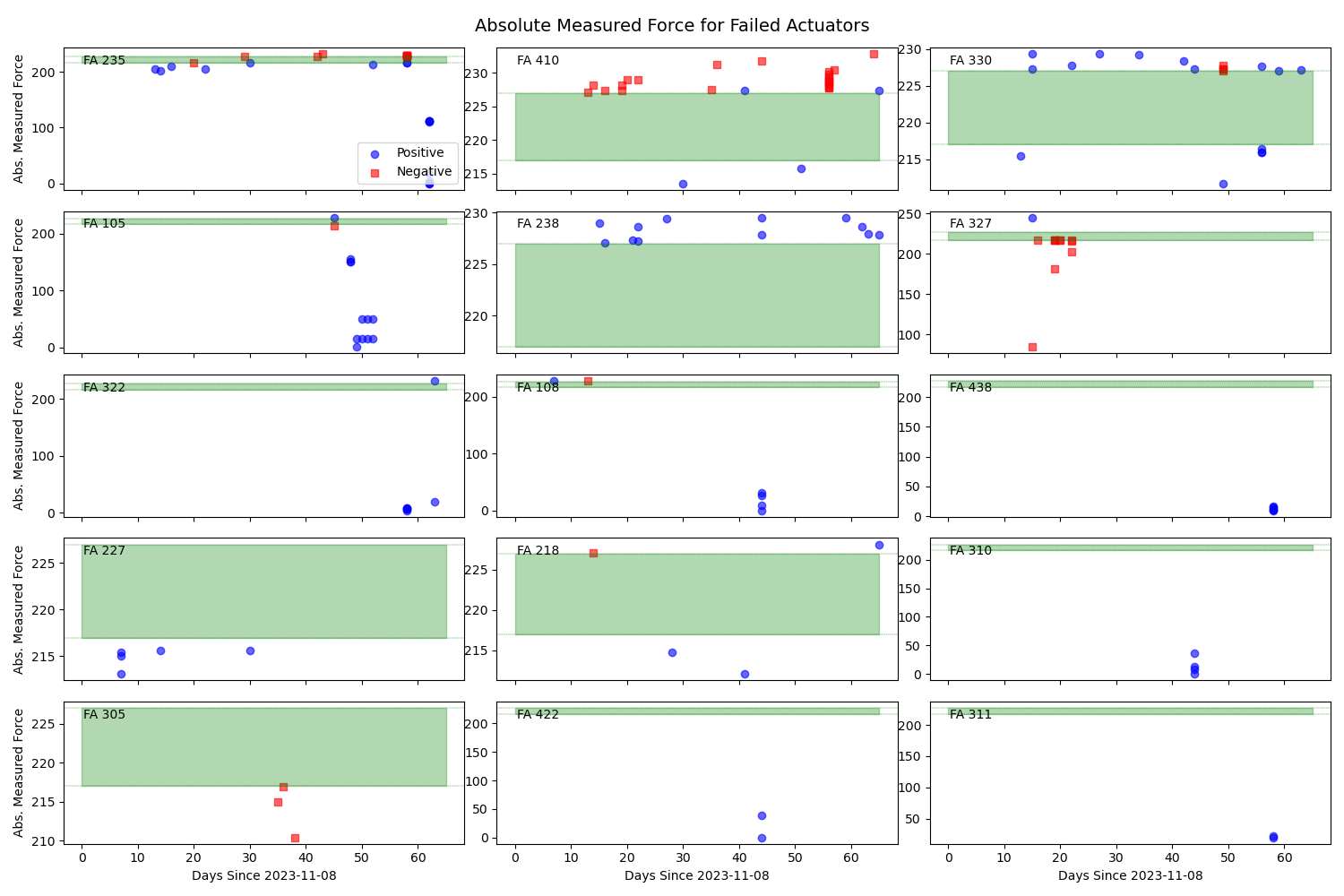
Figure 14. Absolute Measured Force for Failed Actuators.
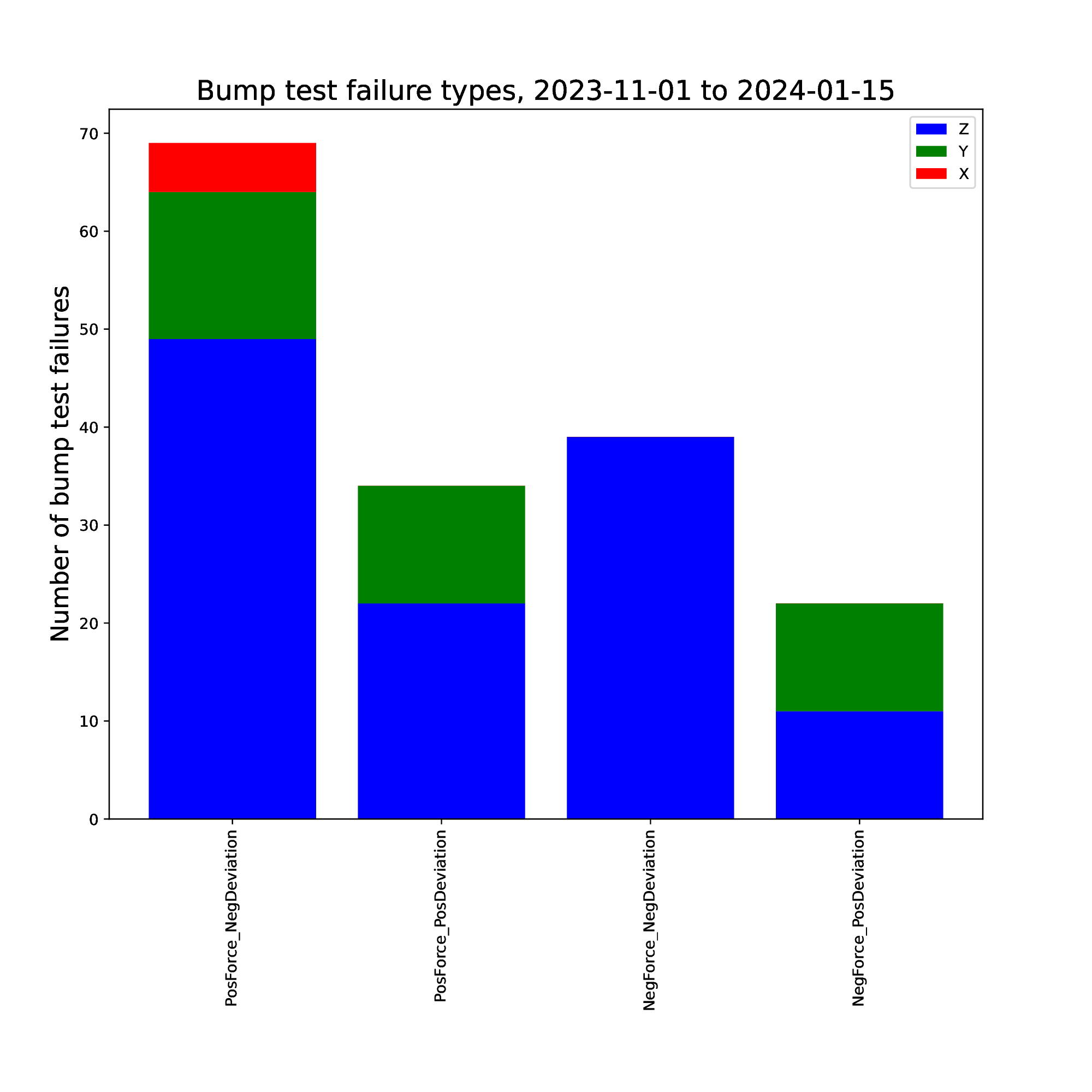
Figure 15. Bump test failure types, 2023-11-01 to 2024-01-15.
actual force overshoot compared to the demanded force: about 23%
actual force undershoot compared to the demanded force: about 74%
excessive latency of the actual force compared to the demanded force: None seen
locked/constant force independent of demand: about 6%
Table 3: Statistics of bump test failure
Summary#
This technote describes the M1M3 mirror cell bump tests and describes how they are done and shows some of the results. Most of the plots shown here can be reproduced with the SITCOM_818_SITCOMTN-083.ipynb from the lsst-sitcom/notebooks_vandv github repository.
The plots showing the rate of failures are part of the notebook SITCOMTN-083_m1m3_bump_test_failure_analysis.ipynb from lsst-sitcom/notebooks_vandv github repository.
The plots in the last section showing the fail statistics were generated with SITCOM-1165_m1m3_bump_test_error_and_measured_forces.ipynb from lsst-sitcom/notebooks_vandv github repository.